大学MOOC 算法设计与分析(淮阴师范学院)1450437204 最新慕课完整章节测试答案
第三周分治策略1
作业测验
1、单选题：
双Hanoi塔问题是Hanoi塔问题的一种推广，与Hanoi塔的不同点在于：2n个圆盘，分成大小不同的n对，每对圆盘完全相同。初始，这些圆盘按照从大到小的次序从下到上放在A柱上，最终要把它们全部移到C柱，移动的规则与Hanoi塔相同。BiHanoi(A, C, n)的功能是从A移动2n个盘子到C，其中BiMove(A, C)表示从A移动两个盘子到C。下列哪一段代码是利用分治策略给出的正确的移动策略：
选项：
A: 
B: 
C: 
D: 
答案: 【 】
2、单选题：
给定n个不同数的数组S和正整数i，
，求S中最大的i个数，并且按照从大到小的次序输出，现有如下算法，
算法：调用i次找最大算法Findmax，每次从S中删除一个最大的数。该算法在最坏情况下的时间复杂度是：
选项：
A: 
B: 
C: 
D: 
E: 
答案: 【 】
3、单选题：
给定n个不同数的数组S和正整数i，
，求S中最大的i个数，并且按照从大到小的次序输出，现有如下算法，
算法：对S排序，并输出S中最大的i个数。该算法在最坏情况下的时间复杂度是：
选项：
A: 
B: 
C: 
D: 
E: 
F: 
答案: 【 】
4、单选题：
有n个砝码（其中n为2的幂，即
），每个重g克，其中一个不合格(重量可能大于或小于g克). 有一个秤可以称出重物的准确重量. 假设所有的砝码可以同时放到秤上，设计一个算法找出这个不合格的砝码，且秤重的次数达到最少. 采用分治算法，每次取一半砝码（比如t个）称重，如果恰好重tg克，那么不合格的砝码在剩下的砝码中；否则不合格的砝码就在被称重的砝码中. 设n枚砝码的称重次数是T(n)，关于T(n)的递推方程是:
括号里应该填：
选项：
A: 
B: 
C: 
D:
E: 
答案: 【 】
5、单选题：
在之前n个砝码的题目中（其顺序可能出现在该题之后），在初值T(2)=1条件下，确定：对于给定的n个砝码，找到其中不合格砝码最多需要称重多少次，并选择一个函数填入括号内. 
.
选项：
A:
B:
C: 
D:
E:
答案: 【 】
6、单选题：
设问题P的输入规模是n，下述三个算法是求解P的不同的分治算法.
算法1：在常数时间将原问题划分为规模减半的5个子问题，递归求解每个子问题，最多用线性时间将子问题的解综合而得到原问题的解.
算法2：先递归求解2个规模为n-1的子问题，最多用常量时间将子问题的解综合得到原问题的解.
算法3：在常数时间将原问题划分为规模n/3的9个子问题，递归求解每个子问题，最多用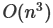
时间将子问题的解综合得到原问题的解.
要求在上述三个算法中选择最坏情况下时间复杂度最低的算法，需要选择哪个算法？
选项：
A: 1
B: 2
C: 3
D: 都不对
答案: 【 1】
7、单选题：
设问题P的输入规模是n，下述三个算法是求解P的不同的分治算法.
算法1：在常数时间将原问题划分为规模减半的5个子问题，递归求解每个子问题，最多用线性时间将子问题的解综合而得到原问题的解.
算法2：先递归求解2个规模为n-1的子问题，最多用常量时间将子问题的解综合得到原问题的解.
算法3：在常数时间将原问题划分为规模n/3的9个子问题，递归求解每个子问题，最多用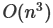
时间将子问题的解综合得到原问题的解.
设最坏情况下时间复杂度最低的算法为A，A在最坏情况下的时间复杂度是
选项：
A: 
B: 
C:
D:
E: 
答案: 【 】
第四周分治策略2
作业测验
1、单选题：
给定含有n个不同的数的数组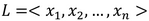
。如果L中存在